Musical interval: What is it, charts, tables, types and characteristics

Musical intervals are the measurement of the distances between notes, and it is a fundamental concept to understand musical theory, we will see the different types, characteristics, tables and charts of musical interval.

What is a musical interval?

An interval is the distance between notes, or put another way, it is the difference in pitch between two tones. Therefore, it is also a relationship between two notes. The definition of musical interval includes both the notes, tones or sounds that sound simultaneously, such as chords, as well as those that sound successively: arpeggios, scales, melodies, and others.

Examples of musical intervals

You have probably heard phrases like: “Between the notes of this guitar melody there is a diminished seventh interval”; “This chord is formed by an interval of Major third and another of Perfect fifth”. These phrases indicate musical intervals used in songs, melodies, or chords.

Below you can see an example of intervals of successive notes and simultaneous notes:

Maybe before starting this tutorial you want to learn how to read sheet music: learn to read guitar music.

How is a musical interval measured?

So, once we know what a musical interval is, the question is how do we measure this difference in height of musical notes? Or simply, how do we measure an interval?

The answer is really simple, to measure a musical interval, we must count tones and semitones that exist between the two musical notes that make up the interval. Later we will see the types of intervals, tables and more.

You are probably wondering now what is a tone? and a semitone?

What is a tone and a semitone?

In a simple way, we can define that a semitone is the distance between two successive notes. This is also valid for two successive frets of the guitar. On the other hand, a tone (T) is the distance formed by two semitones (ST). Thus Western musical notes are separated by semitones, and two semitones make a tone ( ST + ST = T ). For example, between C and C# there is a semitone, and between C and D there are two semitones, or more precisely, one tone.

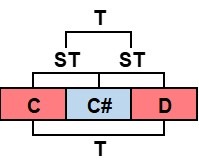
Semitone

The semitone is the minimum distance between two notes. On a guitar, a semitone (ST) is the distance between two successive frets. There is also a semitone distance between the open string and the first fret.

There are two types of semitones:

• Chromatic semitone
• Diatonic semitone

Chromatic semitone

The Chromatic Semitone is one whose two notes that form the semitone interval have the same name. For example, C-C#, G-Gb, D-D#, F-Fb, etc.

Diatonic semitone

The diatonic semitone is one in which the two notes that make up the semitone interval have different names. For example, C-Db, G-F#, B-C, E-F, etc.

As you can see the difference between diatonic and chromatic semitone is written and not voiced.

Tone

A tone is equal to two semitones, that is, on a guitar it is the distance of two frets. For example, between fret 1 and 3 there is a tone, or we could also say two semitones. The same goes for the open string and fret two.

Summarizing: 1 Tone = 2 Semitones.

If we take as a base the natural notes -without including the altered notes-, that is to say the C Major scale, the distances between the notes are the following: T – T – ST – T – T – T – ST

On the piano this is clearly seen, since the white or ivory keys are the natural notes and the black keys are the altered or harmonic notes.

We recommend that you watch our CAGED System for Guitar: Playing Chords Across the Fretboard tutorial.

Numbering and qualification of a musical interval

Normally, a musical interval is not named according to the tones and/or semitones that it has, even if it is a valid form, but according to the distance notes. When we talk about notes we refer to the notes of the scale in which we are playing; thus, in the C major scale, we will use the numerical order of the 7 natural notes: C – D – E – F – G – A – B, as opposed to the 12 notes -semitones- that exist. Thus, between C and D, if we are in the major scale, the interval is 2 because D is the second note. In this way, the C – D interval is 2nd.

But then why did we see the concept of tone and semitone? The tones and semitones will indicate the type of interval: Major, Minor, Perfect, Augmented or Diminished.

How are musical intervals numbered?

The numbering of an interval is done by counting the number of notes it covers, that is, including the notes that make up that interval. As we saw above, in the interval of C and D is 2nd, since C is the first note and C is the second, the interval is 2nd.

Below, we find another musical interval that goes from G to E.

Numbering a musical interval

These notes may or may not be altered depending on what scale the melody is in. Now, as the notes from which we start to number the interval can be altered, with the number we do not really know exactly the number of tones and semitones that exist between the interval.

Seeing the examples of the previous image, you will be able to see that while between C and E there is a 3rd and the distance is 2 tones; between C and E flat is also a 3rd interval and yet the distance is 1 tone and 1 semitone. To identify these differences we must qualify the intervals to be able to distinguish them unequivocally.

You may be interested in knowing the best 50 easy Country songs to play on guitar.

How to identify musical intervals?

In addition to the numbering of the intervals, there are also different types or qualifications that can be: Major, Minor, Perfect, Augmented or Diminished.

However, each interval type can have different qualifications:

• The qualifiers Major and Minor are used in seconds (2nd), thirds (3rd), sixths (6th) and sevenths (7th).
• The Perfect qualifier can only be used in fourths (4th), fifths (5th) and eighths (8th).

Major Intervals -M-, Minor -m- and Perfect -P-

Look at the C natural scale:

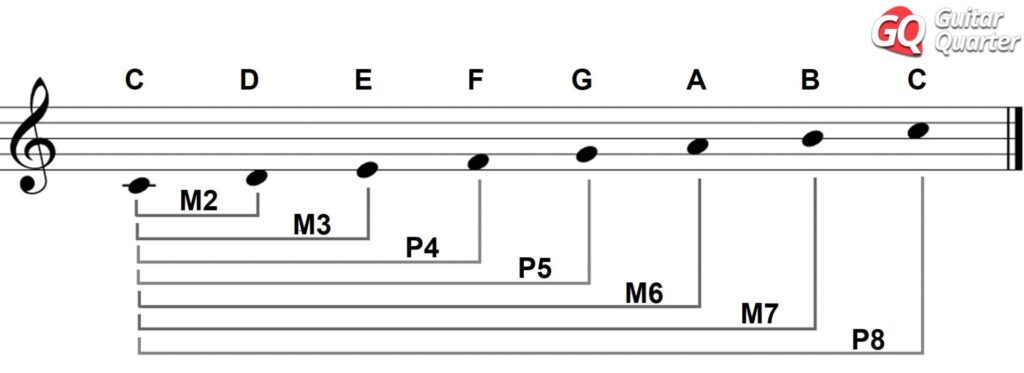
Above in the C Major scale we can see each of the intervals and the distances of whole and semitones:

• Major 2nd = 1 Tone
• Major 3rd = 2 Tones
• Perfect 4th = 2 Tones + 1 Semitone
• Perfect 5th = 3 Tones + 1 Semitone
• Major 6th = 4 Tones + 1 Semitone
• Major 7th = 5 Tones + 1 Semitone
• Perfect 8th = 6 Tones

On the other hand, if we take the natural notes from E we obtain the minor and perfect intervals:

Starting from E and using the natural notes, the intervals and the distance in Tones -or Whole Tones, whole step- and Semitones -or half steps or half tones- are:

• Minor 2nd = 1 Semitone
• Minor 3rd = 1 Tone + 1 Semitone
• Perfect 4th = 2 Tones + 1 Semitone (same as from C)
• Perfect 5th = 3 Tones + 1 Semitone (same as from C)
• Minor 6th = 4 Tones
• Minor 7th = 5 Tones
• Perfect 8th = 6 Tones (same as from C)

Augmented and Diminished Intervals

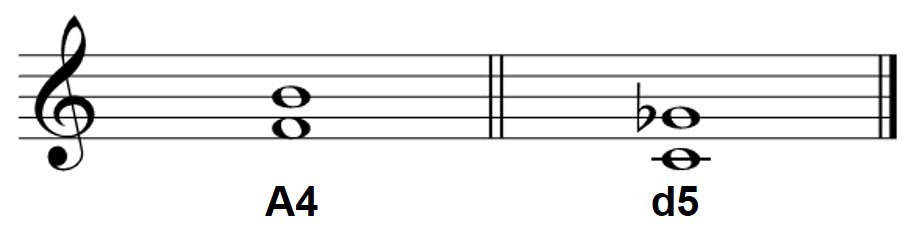
Regarding the qualifiers “Augmented” and “Diminished” they can be used in any interval. Augmented intervals are one semitone higher than their respective Major or Perfect interval. So, below you can see two examples, a perfect fifth interval and its augmented variant, and the same with a major sixth and its respective augmented variant.

Augmented intervals

An Augmented interval can be achieved from a Major or Perfect one of two ways; 1) This is either turning up the top musical note of an interval by a semitone as in the first example below, or 2) lowering the bottom note by a semitone as in the second example below, making the E flat. Thus, with the two options we achieve that the interval is augmented by a semitone.

Diminished intervals

On the other hand, diminished intervals are one semitone less than their respective Minor or Perfect interval. In this way, the diminished intervals are the opposite of the augmented one. Thus, to create a diminished interval from a minor or perfect one we must reduce the interval by a semitone.

As we have seen, it could be done by reducing the upper note by a semitone, for example from G to G flat, or increasing the lower note by a semitone, which would be from F to F sharp.

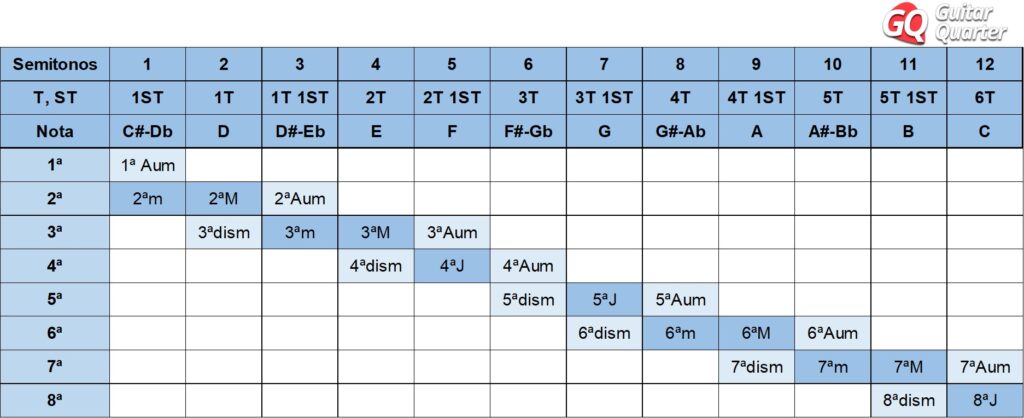
Table of Musical Interval names and short names

Number of semitones	Minor, major, or perfect intervals	Short	Augmented or diminished intervals	Short	Widely used alternative names	Short
0	Perfect unison	P1	Diminished second	d2
1	Minor second	m2	Augmented unison	A1	Semitone, half tone, half step	S
2	Major second	M2	Diminished third	d3	Tone, whole tone, whole step	T
3	Minor third	m3	Augmented second	A2	Trisemitone
4	Major third	M3	Diminished fourth	d4
5	Perfect fourth	P4	Augmented third	A3
6			Diminished fifth Augmented fourth	d5 A4	Tritone	TT
7	Perfect fifth	P5	Diminished sixth	d6
8	Minor sixth	m6	Augmented fifth	A5
9	Major sixth	M6	Diminished seventh	d7
10	Minor seventh	m7	Augmented sixth	A6
11	Major seventh	M7	Diminished octave	d8
12	Perfect octave	P8	Augmented seventh	A7

We recommend that you try the best free online virtual drum machines.

Musical Intervals Chart

To make it easier for us how to name any musical interval that is within an octave there is the Musical Interval Chart Guide. The Musical Intervals Chart is a more effective and easier way to identify intervals and relate them to each other.

Below you can see the scheme to qualify an interval:

As you can see, all the minor intervals have a semitone less than their respective majors. For example, a Major 3rd has 2 whole steps while a minor 3rd has 1 whole step and 1 semitone.

Below we can see the chart of musical intervals. It is assembled by calculating the distances that exist in tones and semitones for each type of interval. Thus, you can see each interval numbered and qualified.

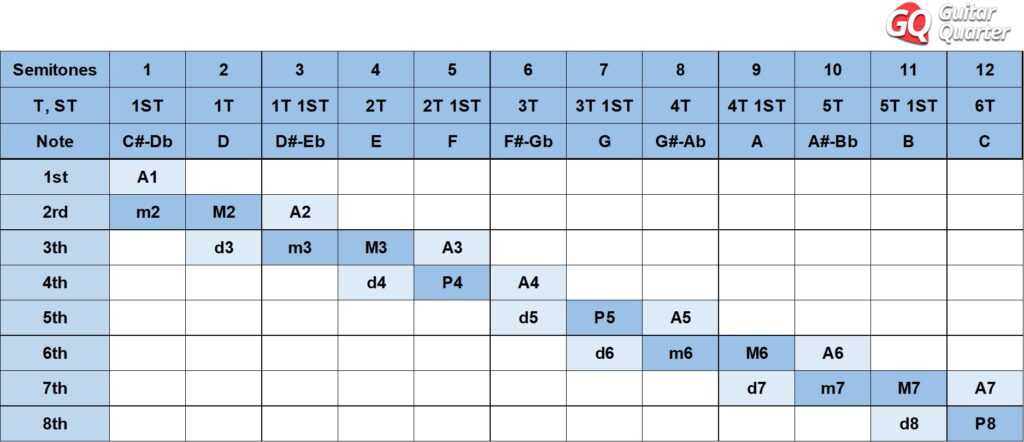
In this musical interval chart you will find all the distances that exist from the note C to any other up to an 8th.

Some of these intervals have very common names, such as the “tritone” case, which is when there is a distance of 3 tones, as is the case of an interval of an augmented 4th or diminished 5th. Also, when we say an 8th we mean a Perfect 8th, since there is also the augmented and diminished 8th. The same thing also happens with the intervals of 4th and 5th, and other cases that we will see below.

Don’t miss the best free and paid VST amp simulators.

Particular cases of musical intervals

Unison

Two notes with the same name and sound are called unison. That is, if two instruments play the same note or if an instrument plays a note followed by the same note, a unison is formed. Thus the unison itself does not constitute an interval, since there is no distance between the notes.

A well-known example is Beethoven’s 5th Symphony, which is based on the constant repetition of three unisons:

Enharmony

An enharmony occurs between two notes that have the same sound and a different spelling or name. As in unison, since there is no distance between two enharmonic notes, it is not considered an interval.

For example, D sharp and E flat are enharmonics; thus they refer to the same sound, but their name is different. In this way, you can see in the chart of musical intervals the cases in which a sound can be called differently: C#-Db, D#-Eb, F#-Gb, G#-Ab and A#-Bb.

You can also see that for each sound you have two possible intervals, for example for C-D that is one tone away, the interval can be a Major 2nd or Diminished 3rd. Also, if we take C-A#/Bb that there are 5 tones apart, the two possible intervals are the Augmented 6th or the Minor 7th.

Why can the same pitch of sound be called by two different names? Later, when we see the concept of tonality, we will explain it; An enharmonic is used to link two sections in apparently very different keys, simply by substituting a note for its enharmonic.

How can we know what possible interval it is?

The interval will depend on the way you call the note. An example would be:

• If the interval is C – A#, it would be an augmented 6th, since from C to A there are 6 notes apart.
• If the interval is C – Bb, it would be a minor 7th, since from C to B there are 7 notes apart.

1st interval

The 1st interval is between notes of the same name. It comes into existence as an augmented 1st and is equivalent to a chromatic semitone. Below you can see two examples on the staff:

2nd diminished

A diminished second does not actually constitute an interval, since there is no distance between the notes. Thus a diminished 2nd is an enharmonic.

If you like to record at home, we recommend the best DAW for your Home Studio.

Classification of musical intervals

Ascending and descending intervals

The ascending and descending intervals are defined based on whether the second note is higher -ascending- or if it is lower -descending-.

Ascending intervals

The ascending intervals occur between two successive sounds when the second is higher than the first.

Descending intervals

The descending intervals are when the second sound is lower than the first.

Steps and Skips

Step and Skip intervals refer to the distance between the two sounds. If the sounds are immediate, it is a Step. On the other hand, if the sounds are not successive and there is a Skip.

Step intervals

Steps are intervals, whether with or without accidentals, between two consecutive notes of a scale. Thus, the Steps are those of seconds. For example: C-D, E-F, G-La, B-C, F-E, etc.

Skip intervals

Skips are intervals that the successive order is not followed. Thus, the Skip intervals are those of 3rd, 4th, 5th, 6th, 7th, etc.

Do not miss our selection of the best easy songs to play on guitar.

Melodic and harmonic musical intervals

The Melodic and harmonic intervals refer to whether the interval is made up of two single notes -melodic- or if more than one note sounds like a chord -harmonic-.

Melodic intervals

The Melodic intervals are formed by two sounds, one after the other, as in a melody.

Harmonic intervals

Harmonic intervals occur when there is more than one sound sounding simultaneously one after the other. Thus, harmonic intervals are counted from the lowest note to the highest or from the bottom to the top in the score.

Simple and compound intervals

The simple and compound intervals are defined according to whether they are between the perfect octave or not. If the interval is up to the Perfect 8th., it is a simple interval. On the other hand, if it is greater than the P8, it is a compound interval.

Simple intervals

A simple interval is when it is within the distance of a perfect octave (P8). Thus, the intervals of 2nd, 3rd, 4th, 5th, 6th, 7th and 8th are simple intervals.

Compound intervals

A compound interval is one that has an amplitude greater than a perfect 8th. Thus, the intervals of 9th, 10th, 11th, 12th, 13th, 14th, 15th, etc., are compound intervals.

Compound intervals are graded the same as their associated simple interval. This is subtracting an octave or subtracting 7 from the compound interval. Thus, an interval composed of 10ths, the simple associate is that of 3rds. If the 3rd interval is minor, the 10th interval will also be minor, that is, it will be a m10.

For example, the simple interval that corresponds to an interval of m10 would be a m3:

Table of compound intervals and their associated simple

Compound interval	Associated Simple
9th	2nd
10th	3rd
11th	4th
12th	5th
13th	6th
14th	7th

You might be interested in a guide on the best cheap studio monitors for your Home Studio.

Consonant and dissonant intervals

Musical intervals are also classified as consonant or dissonant. While the consonant intervals generate a sensation of stability and rest; dissonants generate a feeling of instability and the need for a resolution -normally in a consonant interval-.

Consonant intervals

The consonant intervals sound stable and complete, thus generating a sensation of sound rest in the ear. Within the consonances we find the intervals of 3rd and 6th both Major and minor and the Perfect intervals: 4th, 5th and 8th.

Perfect, invariable, or tonal consonance

The intervals of perfect consonance are those of Perfect 4th, 5th and 8th. Thus, the very word Perfect gives the perfect and invariable character. In addition, its tonal character is given by the fact that degrees I, IV and V of the scale are the tonal degrees, that is, those that define the tonality.

Imperfect, variable or modal consonance

The intervals of imperfect consonance are those of 3rd and 6th, both major and minor. It is precisely this variability between major and minor that makes the consonance imperfect or variable. In turn, it is modal because degrees III and VI of the scale are the ones that most strongly define the major or minor modality.

Dissonant intervals

A dissonant interval sounds unstable and generates sound tension by suggesting a resolution or continuation in a consonant interval. The dissonant intervals are the Major and Minor 2nd and 7th, and all augmented and diminished intervals.

Absolute or diatonic dissonance

The intervals with absolute dissonance are those of 2nd and 7th, both major and minor, and the augmented or diminished intervals in which, even when in harmony, the dissonant character is maintained. Thus, for a dissonance to be absolute, it must ‘resist’ inversion and enharmonization.

Semiconsonances or relative or conditional dissonance

Semiconsonances or relative or conditional dissonances generate a somewhat imprecise auditory sensation, which is neither consonance nor dissonance. These are the augmented 4th and its inversion, the diminished 5th. These intervals have the same extension of 3 tones: C-F# and C-Gb. Thus, relative semiconsonances or dissonances are those augmented or diminished intervals in which, by harmonizing one of its sounds, the interval becomes a consonant. In this way, there is a more apparent than real dissonance conditioned to the tonal context in which it is found.

You may be interested in learning the best famous and easy guitar riffs with Tab.

Inversion of musical intervals

The inversion of musical intervals consists of turning the lower note into the higher one, and the upper note becomes the lower note; in other words, reverse two notes.

How is the inversion of musical intervals carried out?

Below you can see two investment examples. The first consists of raising the lower note of the interval by an 8th. The second what it does is lower the top note by an 8th. Thus, the C-E interval becomes E-C.

Tricks to remember the inversion of a musical interval

There are two very practical tricks to remember the inversion of an interval.

Interval Inversion Trick 1

An interval and its inversion always add up numerically to a 9th. It means that a 2nd will become a 7th, a 3rd will become a 6th, a 4th will become a 5th, a 5th will become a 4th, and so on. The inversion of an 8th would be unison.

Normal	Unison	2nd	3rd	4th	5th	6th	7th	8th
Investment	8th	7th	6th	5th	4th	3rd	2nd	Unison
Addition	9	9	9	9	9	9	9	9

Interval Reversal Trick 2

The classification of an interval and its inversion are opposites. Thus, for a minor interval, its inversion is Major, a Diminished interval, its inversion is an Augmented and so on, except with a Perfect degree which remains Perfect. Below you can see the table that summarizes the relationships of types of musical intervals:

Normal	Inversion
Minor	Major
Diminished	Augmented
Perfect	Perfect
Augmented	Diminished
Major	Minor

Examples of investments in which they look like:

• A M3 when inverted becomes a m6: 3+6=9 and the M becomes m.
• The same happens with a P4 that is inverted into a P5: 4+5=9 and P stays on P.
• Finally, a A2 Inc becomes a d7: 2+7=9 and an Aug becomes a Dim.

Intervals in scales

​By now you should know that the distances between the notes of a scale are fixed. In case you don’t know, we suggest you read this tutorial on guitar scales for beginners.

On a larger scale, the distances between one note and the next are: T – T – ST- T – T – T – ST; no matter what note you start building it with, you will always have to follow the same order of intervals. If you start on C, it will be the C major scale, if you start on D, the D major scale, and so on.

Write the distances between notes of the major scale with intervals

Writing the distances of the larger scale as an interval is: 2ªM – 2ªM – 2ªm – 2ªM – 2ªM – 2ªM – 2ªm. Here we write the interval in relation to each of the previous notes. In addition we can write the intervals with respect to the fundamental -first note-. Thus, the example of a major scale would be: 2ªM – 3ªM – 4ªJ – 5ªJ – 6ªM – 7ªM – 8ªJ.

Major Scale

Below you can see the C Major scale, indicating the distances that exist between each note expressed in tones and semitones, and intervals.

Thus, counting the tones and semitones, we can find the intervals that exist with the first or fundamental note, in this case C:

Notes	Distance	Intervals
C – D	1T	Major 2nd
C – E	2T	Major 3rd
C – F	2T, 1ST	Perfect 4th
C – G	3T, 1ST	Perfect 5th
C – A	4T, 1ST	Major 6th
C – B	5T, 1ST	Major 7th
C – C’	6T	Perfect 8th

Minor Scale

Below you can see the scale of C minor, indicating the distances that exist between each note expressed in tones and semitones, and intervals.

Thus, counting the tones and semitones, we can find the intervals that exist with the first or fundamental note, in this case Cm:

Notes	Distance	intervals
C – D	1T	Major 2nd
C – Eb	1T, 1ST	minor 3rd
C – F	2T, 1ST	Perfect 4th
C – G	3T, 1ST	Perfect 5th
C – Ab	4T	minor 6th
C-Bb	5T	minor 7th
C – C’	6T	Perfect 8th

Differences between C Major and C minor

As you have seen, the differences between the C Major and C minor scales are the intervals of 3rd, 6th and 7th:

If you want to know more about musical harmony, we recommend that you learn Music Modes: 7 Modal Scales and Relation To Chords.

Intervals in chords

Here we are going to see the relationship of intervals and chords by exemplifying it with two of the most common triad -3 note- chords: the perfect major and perfect minor chords.

Intervals in Perfect Major chord

Below we include the C Perfect Major chord, summarized in “PM”. The C PM is composed of C-E-G. When listening to a 3-note chord or triad chord, we can set up to 3 different harmonic intervals that occur simultaneously. In this case the intervals are:

Thus, the intervals in a perfect major chord or PM are:

• Lower note – intermediate note: In C PM, this interval is made up between the fundamental (C) and the M3 (E).
• Lower note – upper note: In C PM, this interval is made up between the fundamental (C) and the P5 (G).
• Intermediate note – top note: In C PM, this interval is between the 3rd (E) and the 5th (m3) (G).

Intervals in perfect minor chord

Below we include the C Perfect minor chord, summarized in “Pm”. The C Pm is composed of C-Eb-G. When listening to a 3-note chord or triad chord, we can set up to 3 different harmonic intervals that occur simultaneously. In this case the intervals are:

Thus, the intervals in a chord of C perfect minor or Pm (C-Eb-G) are:

• Lower note – intermediate note: In C Pm, this musical interval is made up between the fundamental (C) and the m3 (Eb).
• Lower note – upper note: In C Pm, this musical interval is made up between the fundamental (C) and the P5 (G).
• Intermediate note – top note: In C Pm, this musical interval is made up between the 3rd (Eb) and the 5th (M3 – G).

Normally when we talk about the intervals that occur within a chord, we refer to those that occur between the lowest note with the intermediate note and the highest note, so that you will see things written like:

• PM chord: M3 + P5
• Pm chord: m3 + P5

It is a good way to remember the intervals that are formed in a chord, since the last interval we have seen can be deduced from the first one. For example, in the two chords that I have presented to you, if the first 3rd is major, the second 3rd is minor; since it has to be located in the space that remains until a Perfect 5th. In turn, if the first 3rd is a minor, the second is a major 3rd.

Trick to recognize Perfect Major (PM) and Perfect Minor (Pm) chords

Thus, a trick to identify a perfect major chord (PM) or a perfect minor chord (Pm) is to look at the first 3rd, that is, between the bass and the intermediate note. If the third is minor, the chord is perfect minor (Pm); on the other hand, if the 3rd is major, the chord will be perfect major (PM).

You might be interested in our Guitar String Names: Notes, Numbers, and Order tutorial.

Intervals in 4-note chords

Four-note chords are more complex, as we go from three intervals -in 3-note chords- to six. So, below you can see an example of all the intervals in a 4-note chord:

The most relevant intervals are the first 3 that are formed with the lowest note.

Musical intervals in chords with more than 4 notes

Although they are not the most common, there are 5 and 6 note chords. 5-note chords have 10 intervals. While 6-note chords have 15 intervals. Below you can find an example of a five-note chord and the ten intervals it contains:

Musical interval exercises

Exercise 1: Musical Interval of C – G

What type of interval is the following?

Since the notes are C and G, we are talking about a 5th interval. Remember the following musical intervals table:

In the muscial intervals table we can see that between C and G there are: C-D-E-F-G, that is, five notes away. As we have already seen and can be seen in the musical interval table, in natural scales, the 5th that is formed is Perfect. In this way it is an interval of Perfect 5th.

Also, it is an ascending interval, since the 2nd note is higher. Also, it is a simple musical interval because it is within an octave. Additionally, it is a melodic interval, since first one note sounds, then another. As there is more than one note of distance, it is a skip interval -it is not a 2nd-. Finally, the interval corresponds to a perfect consonance because it is a Perfect 5th.

Summarizing, the C – G interval is:

• Ascending
• Simple
• Melodic
• Skip
• Perfect consonant

Do not miss our guide to the sizes of electric, acoustic and classical guitars for children and adults.

Exercise 1: Musical Interval of C – G#

Again we see the notes are C and G, only this time it is a G#. Thus, we are talking about an interval of 5th, but here the G appears with a sharp, that is, one semitone more. Therefore it is an interval of augmented 5th.

This is a resource that we recommend to analyze the intervals: compare any interval with what would be normal in a natural scale Major or minor, and see if it has the same width or not. When it is “normal” the interval will be Major, minor or perfect, otherwise it will be an augmented or diminished interval.

Furthermore, as we have already seen, it is an ascending, simple, melodic, skip interval, but unlike the previous case, the interval corresponds to a semiconsonance.

Summarizing, the interval of C – G# is:

• Ascending
• Simple
• Melodic
• Skip
• Semiconsonant

Summary of musical intervals

Musical interval is the first step in learning harmony. Also, we could say that intervals are the bricks with which harmony is built, and that they shape our musical Chords and Scales.

Do not miss our post of the best Gibson Guitarists: Les Paul, SG and other models.